Formación de la Matriz de Admisión de Autobuses (Yautobús)
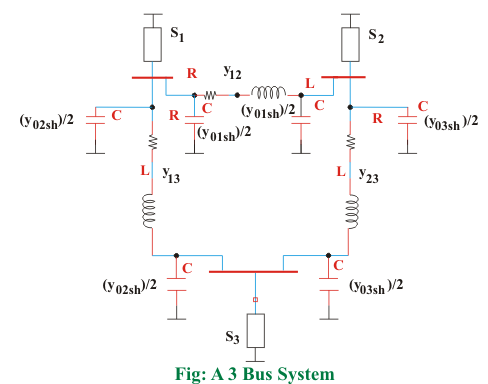

S1, S2, S3 son inyecciones de energía complejas netas en el bus 1, 2, 3 respectivamente
y12, y23, y13 son admisiones de línea entre las líneas 1-2, 2-3, 1-3
y01sh/2, y02sh/2, y03sh/2 son de media línea de carga admisión entre las líneas 1-2, 1-3 y 2-3
Las entradas de carga de media línea conectadas al mismo bus tienen el mismo potencial y por lo tanto pueden combinarse en una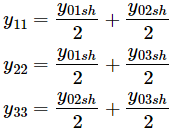
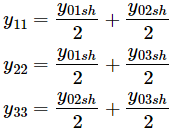
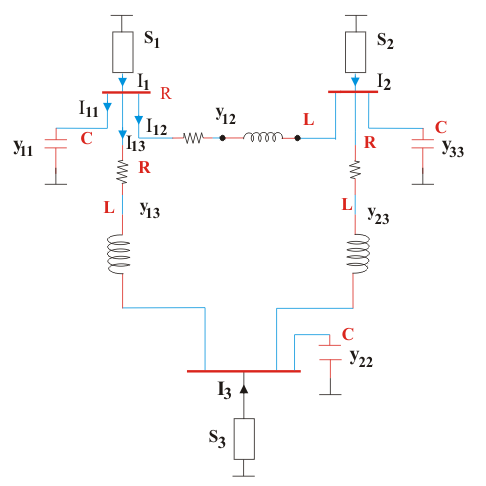

Si aplicamos KCL en el autobús 1, tenemos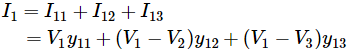
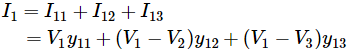
¿Dónde, V1, V2, V3 son voltaje valores en el bus 1, 2, 3 respectivamente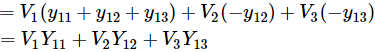
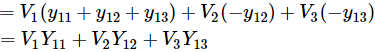
Dónde,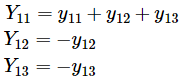
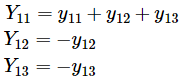
De manera similar, aplicando KCL en los autobuses 2 y 3 podemos derivar los valores de I2 y yo3
Finalmente tenemos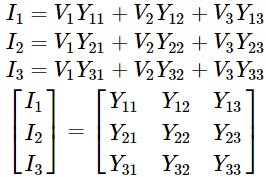
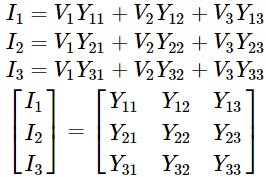
![]()
![]()
En general, para un n sistema de bus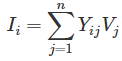
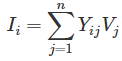
Algunas observaciones sobre el YBUS matriz:
- YBUS es una matriz dispersa
- Los elementos diagonales dominan
- Los elementos fuera de la diagonal son simétricos
- El elemento diagonal de cada nodo es la suma de los admisiones conectado a ella
- El elemento diagonal apagado se niega la admisión
Desarrollo de las ecuaciones de flujo de carga
La inyección de energía compleja neta en el bus i está dada por:
Tomando conjugado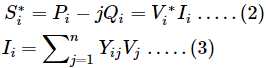
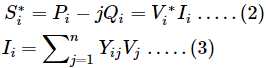
Sustituyendo el valor de Ii en la ecuación (2)
Para derivar la ecuación de flujo de carga estática en forma polar en la ecuación (4) sustituya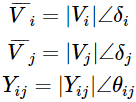
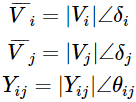
En sustitución de los valores anteriores, la ecuación (4) se convierte en![]()
![]()
En la ecuación (5) al multiplicar los términos se suman los ángulos. Denotemos 
Por lo tanto, la ecuación (5) se convierte en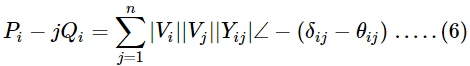
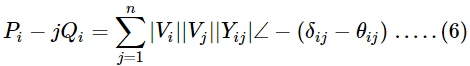
La expansión de la ecuación (6) en términos de seno y coseno da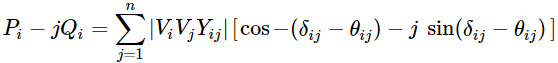
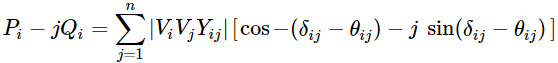
Equiparando las partes reales e imaginarias obtenemos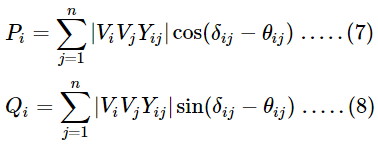
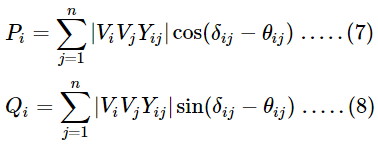
Las ecuaciones (7) y (8) son las ecuaciones de flujo de carga estática en forma polar. Las anteriores ecuaciones obtenidas son ecuaciones algebraicas no lineales y pueden resolverse mediante algoritmos numéricos iterativos.
De manera similar para obtener flujo de carga ecuaciones en forma rectangular en la ecuación (4) sustituyen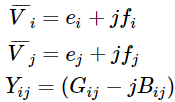
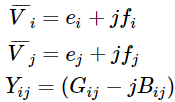
Al sustituir los valores anteriores en la ecuación (4) y al igualar las partes reales e imaginarias obtenemos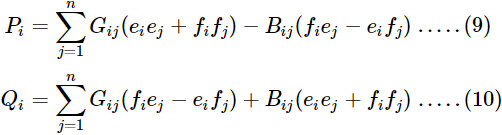
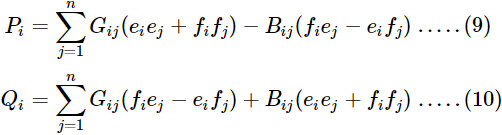
Las ecuaciones (9) y (10) son ecuaciones de flujo de carga estática en forma rectangular.

