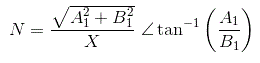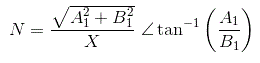El describiendo la función es un procedimiento aproximado para analizar ciertos problemas de control no lineal en ingeniería de control. Para empezar, recordemos primero la definición básica de un sistema de control lineal. Los sistemas de control lineal son aquellos en los que el principio de superposición (si las dos entradas se aplican simultáneamente, entonces la salida será la suma de dos salidas) es aplicable. En el caso de sistemas de control altamente no lineales, no podemos aplicar el principio de superposición.
El análisis de los diferentes sistemas de control no lineales es muy difícil debido a su comportamiento no lineal. No podemos usar métodos de análisis convencionales como el Criterio de estabilidad del níquel o método polo-cero para analizar estos sistemas no lineales, ya que estos métodos están restringidos a los sistemas lineales. Dicho esto, hay algunas ventajas para los sistemas no lineales:
- Los sistemas no lineales pueden funcionar mejor que los lineales.
- Los sistemas no lineales son menos costosos que los lineales.
- Suelen ser pequeños y compactos en tamaño, en comparación con los sistemas lineales.
En la práctica, todos los sistemas físicos tienen alguna forma de no linealidad. A veces puede incluso ser deseable introducir una no linealidad deliberadamente para mejorar el rendimiento de un sistema o hacer más seguro su funcionamiento. En consecuencia, el sistema es más económico que el sistema lineal.
Uno de los ejemplos más simples de un sistema con una no linealidad introducida intencionalmente es un sistema controlado por relés o un sistema ON/OFF. Por ejemplo, en un sistema típico de calefacción doméstica, un horno se enciende cuando la temperatura cae por debajo de un cierto valor especificado y se apaga cuando la temperatura supera otro valor dado. Aquí vamos a discutir dos tipos diferentes de análisis o método para analizar los sistemas no lineales. Los dos métodos se escriben a continuación y se discuten brevemente con la ayuda de un ejemplo.
- Describiendo la función método en el sistema de control
- Método de plano de fase en el sistema de control
No linealidades comunes
En la mayoría tipos de sistemas de controlno podemos evitar la presencia de ciertos tipos de no linealidades. Pueden clasificarse como estáticos o dinámicos. Un sistema para el que existe una relación no lineal entre la entrada y la salida, que no implica una ecuación diferencial, se denomina no linealidad estática. Por otra parte, la entrada y la salida pueden estar relacionadas a través de una ecuación diferencial no lineal. Este sistema se denomina no linealidad dinámica.
Ahora vamos a discutir varios tipos de no linealidad en un sistema de control:
- No linealidad de saturación
- No linealidad de la fricción
- No linealidad de la zona muerta
- La no linealidad de los relés (Controlador ON OFF)
- No linealidad de la reacción
Saturación No linealidad
La no linealidad de saturación es un tipo común de no linealidad. Por ejemplo, véase esta no linealidad en la saturación de la curva de magnetización de Motor de corriente continua. Para entender este tipo de no linealidad, discutamos la curva de saturación o la curva de magnetización que se da a continuación: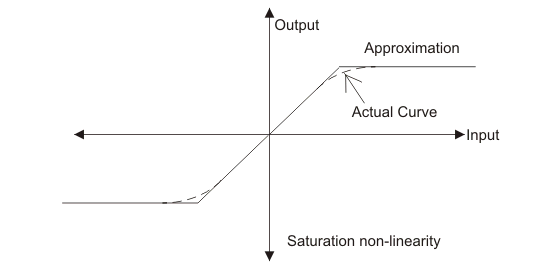

De la curva anterior podemos ver que la salida muestra un comportamiento lineal al principio, pero después de eso hay una saturación en la curva que un tipo de no linealidad en el sistema. También hemos mostrado una curva aproximada.
El mismo tipo de saturación no linealidad también podemos ver en un amplificador para el cual la salida es proporcional a la entrada sólo para un rango limitado de valores de entrada. Cuando la entrada excede este rango, la salida tiende a convertirse en no lineal.
Fricción No linealidad
Cualquier cosa que se oponga al movimiento relativo del cuerpo se llama fricción. Es una especie de no linealidad presente en el sistema. El ejemplo común en un motor eléctrico en el que encontramos arrastre de fricción del culombio debido al contacto de roce entre los cepillos y el conmutador.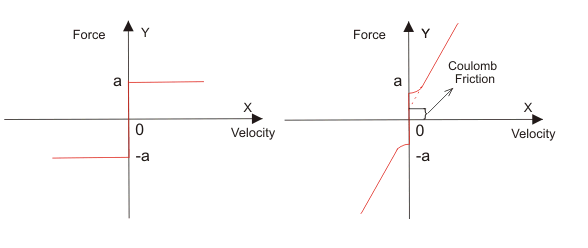

La fricción puede ser de tres tipos y están escritos abajo:
- Fricción estática : En palabras simples, la fricción estática actúa sobre el cuerpo cuando el cuerpo está en reposo.
- Fricción dinámica : La fricción dinámica actúa sobre el cuerpo cuando hay un movimiento relativo entre la superficie y el cuerpo.
- Limitando la fricción: Se define como el valor máximo de la fricción límite que actúa sobre el cuerpo cuando está en reposo.
La fricción dinámica también puede clasificarse como a) Fricción de deslizamiento b) Fricción de rodadura. La fricción de deslizamiento actúa cuando dos cuerpos se deslizan uno sobre el otro mientras que la fricción de rodadura actúa cuando los cuerpos se deslizan sobre otro cuerpo.
En el sistema mecánico tenemos dos tipos de fricción, a saber: a) Fricción viscosa b) Fricción estática.
No linealidad de la zona muerta
La no linealidad de la zona muerta se muestra en varios dispositivos eléctricos como los motores, Los servomotores DC…actuadores, etc. No linealidad de la zona muerta se refieren a una condición en la que la salida se convierte en cero cuando la entrada cruza cierto valor límite.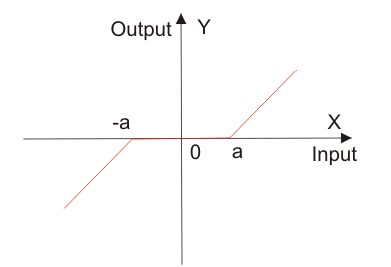

Relés No lineales (Controlador ON/OFF)
Los relés electromecánicos se utilizan con frecuencia en sistemas de control en los que la estrategia de control requiere una señal de control con sólo dos o tres estados. Esto también se llama controlador ON/OFF o controlador de dos estados.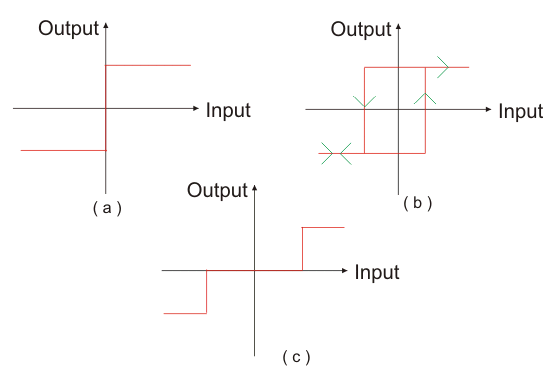

Relé No-Linealidad (a) ON/OFF (b) ON/OFF con Histéresis (c) ON/OFF con Zona Muerta. La figura (a) muestra las características ideales de un relé bidireccional. En la práctica, el relé no responderá instantáneamente. Para las corrientes de entrada entre los dos instantes de conmutación, el relé puede estar en una posición u otra dependiendo de la historia previa de la entrada. Esta característica se denomina ON/OFF con histéresis que se muestra en la Fig (b). Un relé también tiene una cantidad definida de zona muerta en la práctica que se muestra en la Fig (c). La zona muerta es causada por el hecho de que el devanado del campo del relé requiere una cantidad finita de corriente para mover la armadura.
No linealidad de la reacción
Otra importante no linealidad que suele darse en el sistema físico es la histéresis en las transmisiones mecánicas, como los trenes de engranajes y los enlaces. Esta no linealidad es algo diferente de la histéresis magnética y se conoce comúnmente como no linealidad de la reacción. El retroceso es el juego entre los dientes del engranaje impulsor y los del engranaje impulsor. Consideremos que una caja de cambios como la que se muestra en la siguiente figura (a) tiene un juego como el que se ilustra en la figura (b).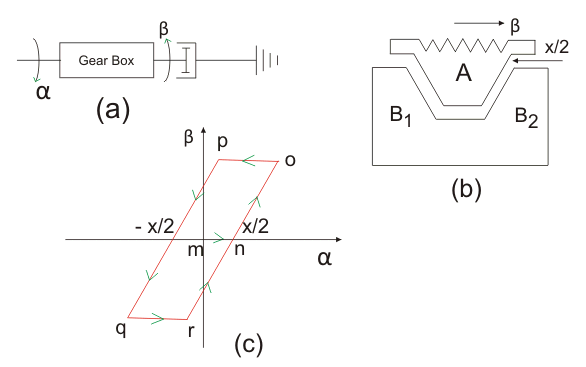

La figura b) muestra los dientes A del engranaje impulsado situados a mitad de camino entre los dientes B1, B2 del engranaje impulsado. La figura (c) da la relación entre los movimientos de entrada y salida. Como el diente A es conducido en el sentido de las agujas del reloj desde esta posición, no se produce ningún movimiento de salida hasta que el diente A hace contacto con el diente B1 del engranaje impulsado después de recorrer una distancia x/2. Este movimiento de salida corresponde al segmento mn de la figura (c). Después de hacer el contacto, el engranaje impulsado gira en sentido contrario a las agujas del reloj a través del mismo ángulo que el engranaje impulsado si se supone que la relación de transmisión es unitaria. Esto se ilustra con el segmento de línea no. Al invertir el movimiento de entrada, el contacto entre los dientes A y B1 se pierde y el engranaje impulsado se vuelve inmediatamente estacionario basándose en la suposición de que la carga está controlada por la fricción con una inercia insignificante.
El movimiento de salida, por lo tanto, provoca que hasta el diente A haya recorrido una distancia x en la dirección inversa como se muestra en la figura (c) por el segmento op. Después de que el diente A establezca contacto con el diente B2el engranaje impulsado ahora se mueve en el sentido de las agujas del reloj, como muestra el segmento pq. Al invertir el movimiento de entrada, la marcha de dirección se detiene de nuevo para el segmento qr y luego sigue a la marcha motriz a lo largo de rn.
Descripción del análisis de la función de los sistemas no lineales
El descripción del método de función en el sistema de control fue inventado por Nikolay Mitrofanovich Kryloy y Nikolay Bogoliubov en el año 1930 y más tarde desarrollado por Ralph Kochenburger.
El describiendo el método de la función se utiliza para determinar la estabilidad de un sistema no lineal de todos los métodos analíticos desarrollados a lo largo de los años para los sistemas de control no lineales, este método es generalmente reconocido como el más útil en la práctica. Este método es básicamente una extensión aproximada de los métodos de respuesta en frecuencia, incluido el criterio de estabilidad de Nyquist, al sistema no lineal.
El describiendo el método de la función de un sistema no lineal se define como la compleja relación de amplitudes y ángulo de fase entre los componentes armónicos fundamentales de la sinusoide de salida y de entrada. También podemos llamar a la función descriptiva sinusoidal. Matemáticamente,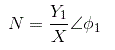
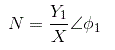
Dónde,
N = describiendo la función,
X = amplitud de la sinusoide de entrada,
Y = amplitud del componente armónico fundamental de la salida,
φ1 = desplazamiento de fase del componente armónico fundamental de la salida.
Discutamos el concepto básico de la descripción de la función del sistema de control no lineal.
Consideremos el siguiente diagrama de bloques de un sistema no lineal, donde G1(s) y G2(s) representan el elemento lineal y N representa el elemento no lineal.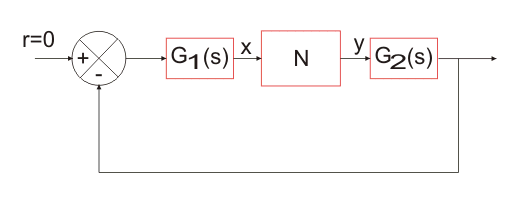

Asumamos que la entrada x al elemento no lineal es sinusoidal, es decir,

Para esta entrada, la salida y del elemento no lineal será una función periódica no sinusoidal que puede expresarse en términos de Series de Fourier como![]()
![]()
La mayoría de las no linealidades son simétricas impares o simétricas de media onda impares; el valor medio Y0 para todos esos casos es cero y por lo tanto la salida será,

Como G1s) G2s) tiene características de paso bajo, puede suponerse con un buen grado de aproximación que todos los armónicos superiores de y se filtran en el proceso, y la entrada x al elemento no lineal N es aportada principalmente por el componente fundamental de y, es decir, los primeros armónicos. Así pues, en el análisis de la función descriptiva, asumimos que sólo el componente armónico fundamental de la salida. Dado que los armónicos superiores en la salida de un sistema no lineal son a menudo de menor amplitud que la amplitud del componente armónico fundamental. La mayoría de los sistemas de control son filtros de paso bajo, con el resultado de que los armónicos superiores están muy atenuados en comparación con el componente armónico fundamental.
Por lo tanto, y1 sólo hay que tenerlo en cuenta.

Podemos escribir y1(t) en la forma,![]()
![]()
Donde usando el fásor,![]()
![]()
El coeficiente A1 y B1 del Series de Fourier se dan por…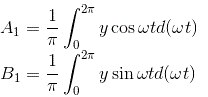
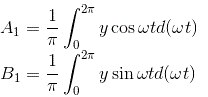
De la definición de la función descriptiva que tenemos,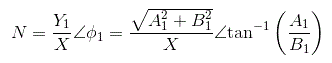
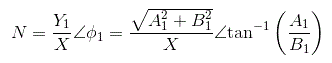
Averigüemos la función descriptiva de estas no linealidades.
Describiendo la función para la no linealidad de saturación
Tenemos la curva característica de saturación como se muestra en la figura dada.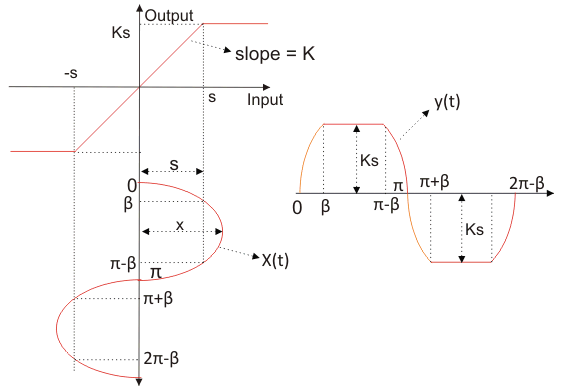

Tomemos la función de entrada como

Ahora desde la curva podemos definir la salida como: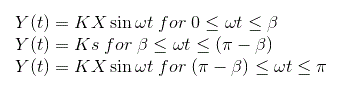
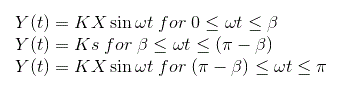
Primero calculamos Series de Fourier La constante A1.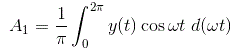
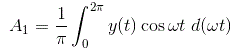
Al sustituir el valor de la salida en la ecuación anterior e integrar la función de 0 a 2 tenemos el valor de la constante A1 como cero.
De manera similar podemos calcular el valor de la constante de Fourier B1 para la salida dada y el valor de B1 se puede calcular como,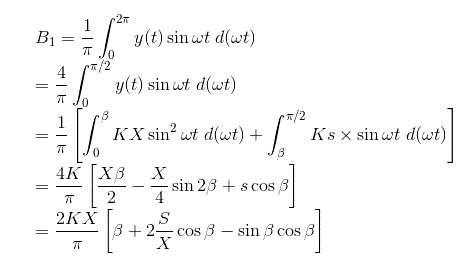
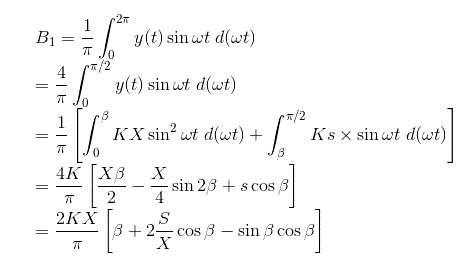
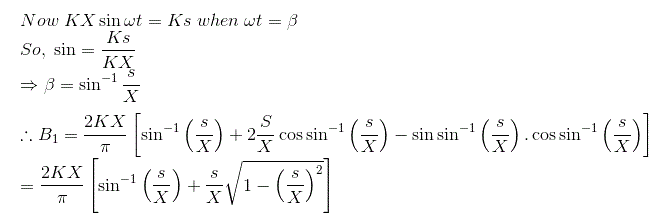
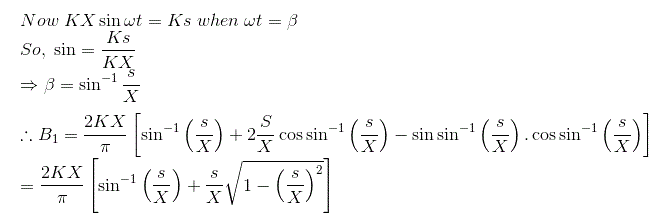
El ángulo de fase para la función descriptiva puede calcularse como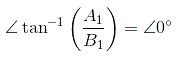
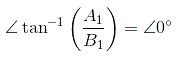
Así, la función descriptiva de la saturación es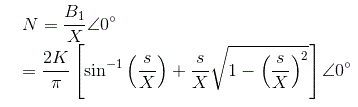
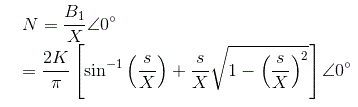
Describiendo la función del relé ideal
Tenemos la curva característica para el relé ideal como se muestra en la figura dada.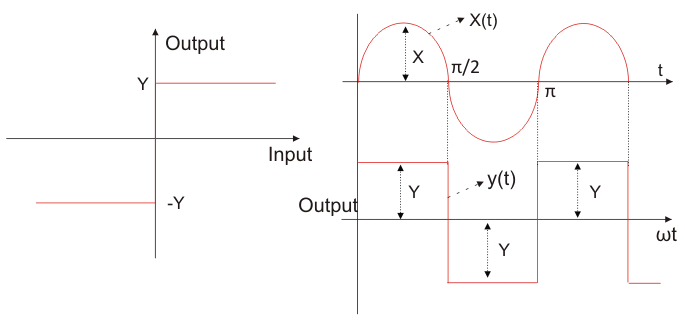

Tomemos la función de entrada como

Ahora desde la curva podemos definir la salida como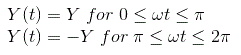
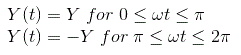
La función periódica de salida tiene una simetría extraña:![]()
![]()
Calculemos primero la constante A de las series de Fourier1.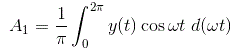
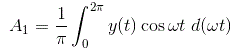
Al sustituir el valor de la salida en la ecuación anterior e integrar la función de 0 a 2 tenemos el valor de la constante A1 como cero.
De manera similar podemos calcular el valor de la constante de Fourier B1 para la salida dada y el valor de B1 puede calcularse como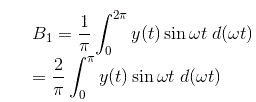
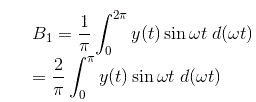
Al sustituir el valor de la producción en la ecuación anterior y(t) = Y tenemos el valor de la constante B1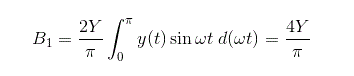
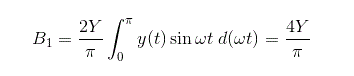
Y el ángulo de fase para la función descriptiva puede ser calculado como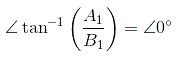
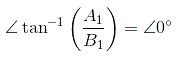
Por lo tanto, la función descriptiva de un relé ideal es![]()
![]()
Describiendo la función del relé real (Relé con zona muerta)
Tenemos la curva característica de la realidad como se muestra en la figura dada. Si X es menor que la zona muerta , entonces el relé no produce ninguna salida; la primera componente armónica de Series de Fourier es, por supuesto, cero y la descripción de la función también es cero. Si X > el relé produce la salida.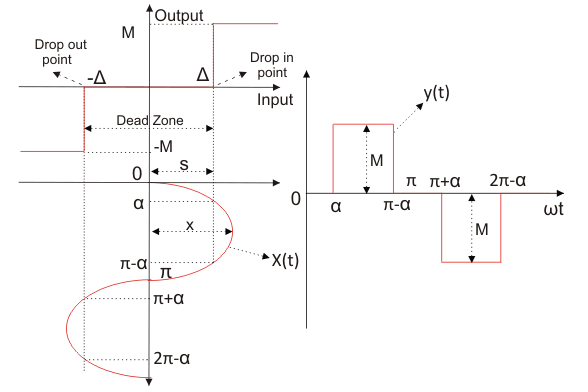

Tomemos la función de entrada como

Ahora desde la curva podemos definir la salida como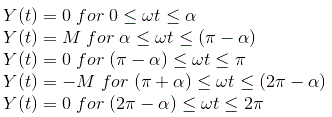
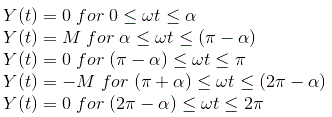
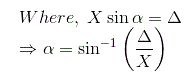
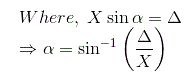
La función periódica de salida tiene una simetría extraña:![]()
![]()
Primero calculamos Series de Fourier La constante A1.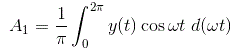
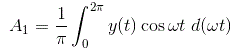
Al sustituir el valor de la salida en la ecuación anterior e integrar la función de 0 a 2 tenemos el valor de la constante A1 como cero.
De manera similar podemos calcular el valor de la constante de Fourier B para la salida dada y el valor de B puede ser calculado como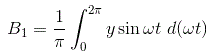
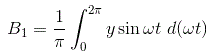
Debido a la simetría de y, el coeficiente B1 se puede calcular de la siguiente manera,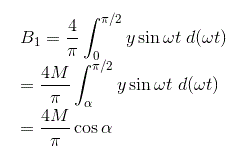
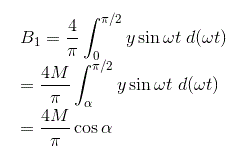
Por lo tanto, la función descriptiva es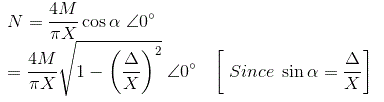
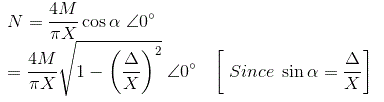
Descripción de la función para la no linealidad del retroceso
Tenemos la curva característica para el retroceso como se muestra en la figura dada. Tomemos la función de entrada como

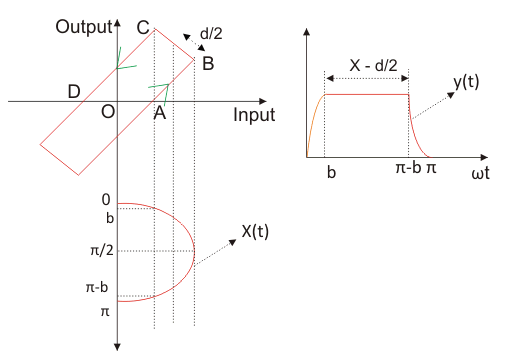

Ahora desde la curva podemos definir la salida como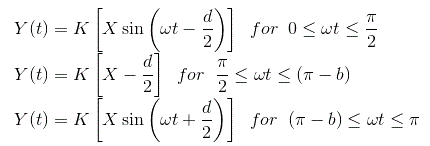
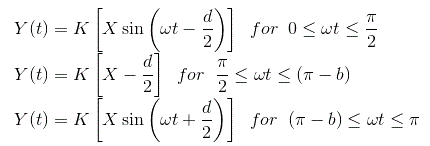
Primero calculamos Series de Fourier La constante A1.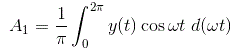
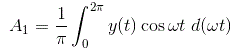
Al sustituir el valor de la salida en la ecuación anterior e integrar la función de cero a 2 tenemos el valor de la constante A1 como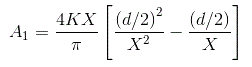
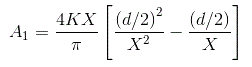
De manera similar podemos calcular el valor de la constante de Fourier B para la salida dada y el valor de B1 puede calcularse como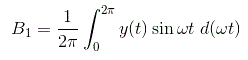
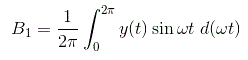
Al sustituir el valor de la salida en la ecuación anterior e integrar la función de cero a pi tenemos el valor de la constante B1 como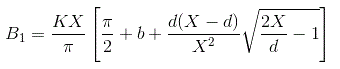
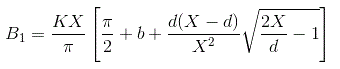
Podemos calcular fácilmente la función descriptiva del retroceso a partir de la siguiente ecuación