Después de leer la teoría de síntesis de la redpodemos decir fácilmente que cualquier polo del sistema se encuentra a la derecha del origen del plano s, lo que hace que el sistema sea inestable. Sobre la base de esta condición A. Hurwitz y E.J.Routh comenzaron a investigar las condiciones necesarias y suficientes de estabilidad de un sistema. Discutiremos dos criterios para la estabilidad del sistema. Un primer criterio es dado por A. Hurwitz y este criterio es también conocido como Criterio Hurwitz de estabilidad o Criterio de Estabilidad de Routh Hurwitz (R-H).
Criterio de Hurwitz
Con la ayuda de la ecuación característica, haremos una serie de determinantes de Hurwitz para averiguar la estabilidad del sistema. Definimos la ecuación característica del sistema como

Ahora hay n determinantes para nth la ecuación característica de orden.
Veamos cómo podemos escribir determinantes a partir de los coeficientes de la ecuación característica. El procedimiento paso a paso para kth La ecuación característica de orden está escrita a continuación:
Determinante: El valor de este determinante está dado por |a1| donde un1 es el coeficiente de sn-1 en la ecuación característica.
Determinante dos : El valor de este determinante viene dado por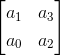
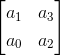
Aquí el número de elementos en cada fila es igual al número determinante y tenemos el número determinante aquí es dos. La primera fila consiste en los dos primeros coeficientes impares y la segunda fila consiste en los dos primeros coeficientes pares.
Determinante tres : El valor de este determinante viene dado por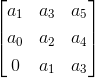
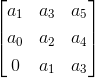
Aquí el número de elementos en cada fila es igual al número determinante y tenemos el número determinante aquí es tres. La primera fila consta de los tres primeros coeficientes impares, la segunda fila consta de los tres primeros coeficientes pares y la tercera fila consta del primer elemento como cero y el resto de dos elementos como los dos primeros coeficientes impares.
Determinante cuatro: El valor de este determinante viene dado por,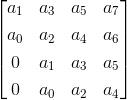
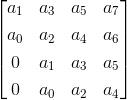
Aquí el número de elementos en cada fila es igual al número determinante y tenemos el número determinante aquí es cuatro. La primera fila consta de los primeros tres cuatro coeficientes, la segunda fila consta de los primeros cuatro coeficientes pares, la tercera fila consta del primer elemento como cero y el resto de tres elementos como los tres primeros coeficientes impares la cuarta fila consta del primer elemento como cero y el resto de tres elementos como los tres primeros coeficientes pares.
Siguiendo el mismo procedimiento podemos generalizar la formación determinante. La forma general de determinante se da a continuación:

Ahora, para comprobar la estabilidad del sistema anterior, calcula el valor de cada determinante. El sistema será estable si y sólo si el valor de cada determinante es mayor que cero, es decir, el valor de cada determinante debe ser positivo. En todos los demás casos el sistema no será estable.
Criterio de Estabilidad de Routh
Este criterio es también conocido como el Criterio Hurwitz modificado de estabilidad del sistema. Estudiaremos este criterio en dos partes. La primera parte cubrirá la condición necesaria para la estabilidad del sistema y la segunda parte cubrirá la condición suficiente para la estabilidad del sistema. Consideremos de nuevo la ecuación característica del sistema como

1) Primera parte (condición necesaria para la estabilidad del sistema): En esto tenemos dos condiciones que están escritas a continuación:
- Todos los coeficientes de la ecuación característica deben ser positivos y reales.
- Todos los coeficientes de la ecuación característica deben ser distintos de cero.
2) Segunda parte (condición suficiente para la estabilidad del sistema): Construyamos primero una matriz de routing. Para construir la matriz de rocas, siga estos pasos:
- La primera fila consistirá en todos los términos pares de la ecuación característica. Ordénelos desde el primero (término par) hasta el último (término par). La primera fila está escrita abajo: a0 a2 a4 a6
- La segunda fila consistirá en todos los términos impares de la ecuación característica. Ordénelos desde el primero (término impar) hasta el último (término impar). La primera fila se escribe a continuación: a1 a3 a5 a7..
- Los elementos de la tercera fila se pueden calcular como:
(1) Primer elemento : Multiplica una0 con el elemento diagonalmente opuesto de la siguiente columna (es decir, un3) y luego restarlo del producto de un1 y un2 (donde un2 es el elemento diagonalmente opuesto de la siguiente columna) y luego finalmente dividir el resultado para obtener con un1. Matemáticamente escribimos como primer elemento
![]()
![]()
(2) Segundo elemento : Multiplica una0 con el elemento diagonalmente opuesto de la siguiente columna (es decir, un5) y luego restarlo del producto de un1 y un4 (donde, un4 es el elemento diagonalmente opuesto del siguiente a la siguiente columna) y luego finalmente dividir el resultado para obtener con un1. Matemáticamente escribimos como segundo elemento![]()
![]()
De manera similar, podemos calcular todos los elementos de la tercera fila.
d) Los elementos de la cuarta fila pueden calcularse mediante el siguiente procedimiento:
(1) Primer elemento : Multiplica b1 con el elemento diagonalmente opuesto de la siguiente columna (es decir, un3) y luego restarlo del producto de un1 y b2 (donde, b2 es el elemento diagonalmente opuesto de la siguiente columna) y luego finalmente dividir el resultado para obtener con b1. Matemáticamente escribimos como primer elemento![]()
![]()
(2) Segundo elemento : Multiplica b1 con el elemento diagonalmente opuesto de la siguiente columna (es decir, un5) y luego restarlo del producto de un1 y b3 (donde, b3 es el elemento diagonalmente opuesto del siguiente a la siguiente columna) y luego finalmente dividir el resultado para obtener con un1. Matemáticamente escribimos como segundo elemento![]()
![]()
De manera similar, podemos calcular todos los elementos de la cuarta fila.
De manera similar, podemos calcular todos los elementos de todas las filas.
Criterios de estabilidad si todos los elementos de la primera columna son positivos, entonces el sistema será estable. Sin embargo, si alguno de ellos es negativo el sistema será inestable.
Ahora hay algunos casos especiales relacionados con los Criterios de Estabilidad de Routh que se examinan a continuación:
(1) Caso uno: Si el primer término de cualquier fila de la matriz es cero mientras que el resto de la fila tiene al menos un término no cero.
En este caso asumiremos un valor muy pequeño () que tiende a cero en lugar de cero. Reemplazando el cero por () calcularemos todos los elementos de la matriz de Routh. Después de calcular todos los elementos aplicaremos el límite en cada elemento que contenga (). Al resolver el límite en cada elemento si obtenemos un valor límite positivo entonces diremos que el sistema dado es estable, de lo contrario en todas las demás condiciones diremos que el sistema dado no es estable.
(2) Caso segundo : Cuando todos los elementos de cualquier fila de la matriz de Routh son cero. En este caso podemos decir que el sistema tiene los síntomas de estabilidad marginal. Entendamos primero el significado físico de tener todos los elementos cero de cualquier fila. El significado físico es que hay raíces simétricas de la ecuación característica en el plano s. Ahora bien, para averiguar la estabilidad en este caso, primero encontraremos la ecuación auxiliar. La ecuación auxiliar puede formarse utilizando los elementos de la fila justo por encima de la fila de ceros en la matriz de Routh. Después de encontrar la ecuación auxiliar, diferenciaremos la ecuación auxiliar para obtener elementos de la fila de ceros. Si no hay cambio de signo en la nueva matriz de Routh formada utilizando la ecuación auxiliar, entonces en esto decimos que el sistema dado es estable limitado. Mientras que en todos los demás casos diremos que el sistema dado es inestable.