En la solución de Redes, Transitorios y Sistemas a veces no nos interesa averiguar toda la función del tiempo f(t) a partir de su Laplace Transformar F(s), que está disponible para la solución. Es muy interesante encontrar que podemos encontrar el primer o el último valor de f(t) o sus derivados sin tener que averiguar toda la función f(t). Nos interesará conocer los valores finales y sus derivados en este artículo.
Por el bien del ejemplo:
Si se da F(s), nos gustaría saber qué es F(), sin conocer la función f(t), que es la Transformación Inversa de Laplace, en el tiempo t . Esto se puede hacer utilizando la propiedad de la Transformación Laplace conocida como Teorema del valor finalTeorema del valor final y teorema del valor inicial se llaman juntos los Teoremas Limitadores.
Definición del teorema del valor final de la transformación de Laplace
Si f(t) y f'(t) ambos son Laplace Transformable y sF(s) no tiene ningún polo en el eje jw y en el R.H.P. (Medio Plano Derecho) entonces,![]()
![]()
Prueba del teorema del valor final de la transformación de Laplace
Conocemos la propiedad de diferenciación de la Transformación de Laplace: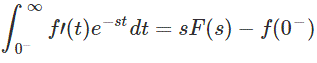
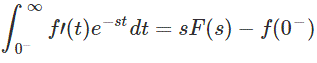
Nota
Aquí el límite 0– se toma para cuidar los impulsos presentes en t = 0
Ahora tomamos el límite como s 0. Luego e-st 1 y toda la ecuación parece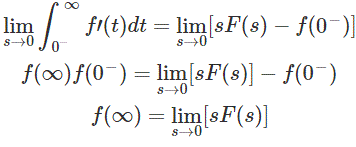
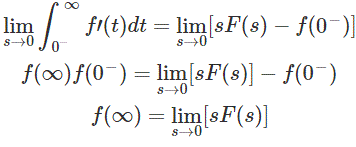
Puntos para recordar:
- Para aplicar el FVT necesitamos asegurarnos de que f(t) y f'(t) son transformables.
- Tenemos que asegurarnos de que el Valor Final existe. El valor final no existe en los siguientes casos
Si el sF(s) tiene postes en el lado derecho del plano del s. [Ejemplo 3]
Si sF(s) tiene polos conjugados en el eje jw. [Ejemplo 4]
Si el sF(s) tiene un polo en el origen. [Ejemplo 5]
- Entonces aplica…
![]()
![]()
Ejemplos del Teorema del Valor Final de la Transformación de Laplace
Encuentra los valores finales de la F(s) dada sin calcular explícitamente la f(t)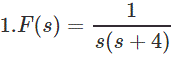
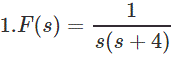
Respuesta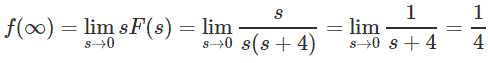
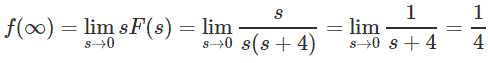
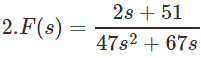
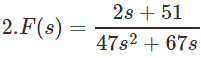
Respuesta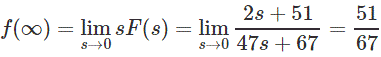
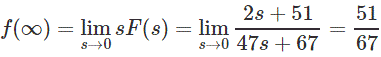
Nota
Ver aquí Transformación Laplace inversa es difícil en este caso. Aún así podemos encontrar el Valor Final a través del Teorema.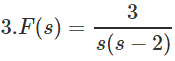
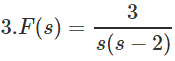
Respuesta
Nota
En los ejemplos 1 y 2 hemos comprobado las condiciones también pero las satisface todas. Así que nos abstenemos de mostrar explícitamente. Pero aquí el sF(s) tiene un polo en el R.H.P como el denominador tiene una raíz positiva.
Así que, aquí no podemos aplicar Teorema del valor final.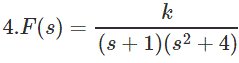
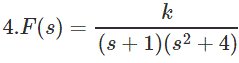
Respuesta
Nota
En este ejemplo sF(s) tiene polos en el eje jw. +2i y -2i específicamente.
Así que, aquí no podemos aplicar Teorema del valor final también.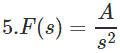
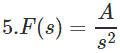
Respuesta
Nota
En este ejemplo sF(s) tiene el polo en el origen.
Así que aquí no podemos aplicar el Teorema del Valor Final también.
Truco final
Sólo comprueba que el sF(s) no tiene límites o no. Si no tiene límite, entonces no es apto para Teorema del valor final y el valor final es simplemente infinito.