Antes de presentarles el concepto de análisis del espacio de estado del sistema de controles muy importante discutir aquí las diferencias entre la teoría convencional de sistema de control y la moderna teoría del sistema de control.
- La teoría de control convencional se basa completamente en el enfoque del dominio de la frecuencia, mientras que la teoría del sistema de control moderno se basa en el enfoque del dominio del tiempo.
- En la teoría convencional de sistema de control tenemos lineal y tiempo invariante de entrada única salida única (SISO), pero con la ayuda de la teoría del sistema de control moderno podemos hacer fácilmente el análisis incluso de sistemas no lineales y de sistemas de entradas múltiples y salidas múltiples (MIMO).
- En la teoría moderna del sistema de control, el análisis de estabilidad y el análisis de respuesta en el tiempo se pueden hacer tanto por el método gráfico como analítico muy fácilmente.
Ahora análisis del espacio de estado del sistema de control se basa en la teoría moderna que es aplicable a todo tipo de sistemas como los sistemas de entrada única y salida única, los sistemas de entrada múltiple y salida múltiple, los sistemas lineales y no lineales, los sistemas con variación de tiempo y los sistemas invariantes de tiempo. Consideremos algunos términos básicos relacionados con el análisis del espacio de estado de la teoría moderna de los sistemas de control.
- Análisis del estado en el espacio de estado: Se refiere al conjunto más pequeño de variables cuyo conocimiento a t = t0 junto con el conocimiento de la entrada de t t0 da el conocimiento completo del comportamiento del sistema en cualquier momento t t0.
- Variables de estado en el análisis del espacio de estado : Se refiere al conjunto más pequeño de variables que nos ayudan a determinar el estado del sistema dinámico. Las variables de estado están definidas por x1(t), x2(t)..Xn(t).
- Vector de Estado :Supongamos que se requieren n variables de estado para describir el comportamiento completo del sistema dado, entonces estas n variables de estado se consideran n componentes de un vector x(t). Dicho vector se conoce como vector de estado.
- Estado del espacio: Se refiere al espacio de n dimensiones que tiene x1 eje, x2 eje xn eje.
Ecuaciones espaciales de estado
Deduzcamos las ecuaciones de espacio de estado para el sistema que es lineal e invariable en el tiempo.
Consideremos el sistema de entradas múltiples y salidas múltiples que tiene r entradas y m salidas.
Donde, r = u1, u2, u3 .. ur.
Y m = y1, y2 .. ym.
Ahora estamos tomando n variables de estado para describir el sistema dado, por lo tanto n = x1, x2, .. xn.
También definimos los vectores de entrada y salida como,
Transponer los vectores de entrada,![]()
![]()
Donde, T es la transposición de la matriz.
Transponer los vectores de salida,![]()
![]()
Donde, T es la transposición de la matriz.
Transponer los vectores de estado,![]()
![]()
Donde, T es la transposición de la matriz.
Estas variables están relacionadas por un conjunto de ecuaciones que se escriben a continuación y que se conocen como ecuaciones del espacio de estado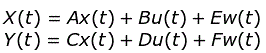
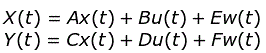
Representación del modelo de Estado utilizando la función de transferencia
Descomposición : Se define como el proceso de obtención del modelo de estado a partir de la función de transferencia dada. Ahora podemos descomponer la función de transferencia de tres maneras diferentes:
- Descomposición directa,
- Descomposición en cascada o en serie,
- Descomposición paralela.
En todos los métodos de descomposición anteriores convertimos primero la función de transferencia dada en las ecuaciones diferenciales, que también se denominan ecuaciones dinámicas. Después de convertir en ecuaciones diferenciales tomaremos la inversa Laplace transformar de la ecuación anterior, que corresponde entonces al tipo de descomposición que podemos crear el modelo. Podemos representar cualquier tipo de función de transferencia en el modelo de estado. Tenemos varios tipos de modelo como el modelo eléctrico, el modelo mecánico, etc.
Expresión de la Matriz de Transferencia en términos de A, B, C y D. Definimos la matriz de transferencia como la transformación Laplace de salida a la transformación Laplace de entrada.
Al escribir de nuevo las ecuaciones de estado y tomar la transformación de Laplace de ambas ecuaciones de estado (asumiendo condiciones iniciales iguales a cero) tenemos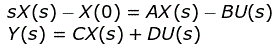
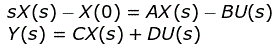
Podemos escribir la ecuación como![]()
![]()
Donde, yo es una matriz de identidad.
Ahora, sustituyendo el valor de X(s) en la ecuación Y(s) y poniendo D = 0 (la media es una matriz nula) tenemos![]()
![]()
El inverso de la matriz puede sustituir por el adj de la matriz dividida por el determinante de la matriz, ahora al reescribir la expresión que tenemos de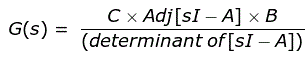
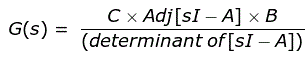
|sI-A|también se conoce como ecuación característica cuando se equipara a cero.
Concepto de valores propios y vectores propios
Las raíces de la ecuación característica que hemos descrito anteriormente se conocen como valores propios o valores propios de la matriz A.
Ahora hay algunas propiedades relacionadas con los valores propios y estas propiedades están escritas abajo…
- Cualquier matriz cuadrada A y su transposición At tienen los mismos valores propios.
- La suma de los valores propios de cualquier matriz A es igual al rastro de la matriz A.
- El producto de los valores propios de cualquier matriz A es igual al determinante de la matriz A.
- Si multiplicamos una cantidad escalar a la matriz A, los valores propios también se multiplican por el mismo valor de escalar.
- Si invertimos la matriz dada A, sus valores propios también se invierten.
- Si todos los elementos de la matriz son reales, entonces los valores propios correspondientes a esa matriz son reales o existen en un par conjugado complejo.
Ahora existe un vector propio que corresponde a un valor propio, si cumple la siguiente condición (ek I A)Pk = 0. Donde, k = 1, 2, 3, ..n.
Matriz de transición de estados y respuesta de estado cero
Estamos interesados en derivar las expresiones para la matriz de transición de estados y la respuesta de estado cero. De nuevo tomando las ecuaciones de estado que hemos deducido anteriormente y tomando su La transformación de Laplace que tenemos,

Ahora, al reescribir la ecuación anterior, tenemos

Dejemos que [sI-A]-1 = (s) y tomando el Laplace inverso de la ecuación anterior tenemos![]()
![]()
La expresión (t) se conoce como matriz de transición de estados.
L-1.(t)BU(s) = respuesta de estado cero.
Ahora discutamos algunas de las propiedades de la matriz de transición de estados.
- Si sustituimos t = 0 en la ecuación anterior, entonces obtendremos 1. Matemáticamente podemos escribir (0) = 1.
- Si sustituimos t = -t en la (t) entonces obtendremos el inverso de (t). Matemáticamente podemos escribir (-t) = [(t)]-1.
- También tenemos otra propiedad importante [(t)]n = (nt).