Síntesis de la red | Polinomio Hurwitz | Funciones reales positivas

Teoría de la síntesis de la red

Funciones de la red

La teoría de la síntesis de redes implica la síntesis de redes compuestas de ambos componentes activos (como resistencias) y componentes pasivos (como inductores y condensadores).

Empecemos con lo básico: qué es una función de la red? En el dominio de la frecuencia, funciones de red se definen como el cociente obtenido al dividir el fásor correspondiente al circuito de salida por el fásor correspondiente al circuito de entrada.

En palabras simples, funciones de red son la relación entre el fásor de salida y el de entrada cuando los fáseres existen en el dominio de la frecuencia. La forma general de las funciones de la red se indica a continuación: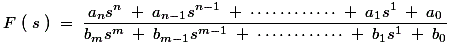

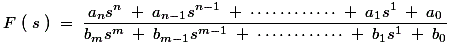
Ahora con la ayuda de la función de red general anterior, podemos describir las condiciones necesarias para la estabilidad de todas las funciones de la red. Hay tres condiciones necesarias para la estabilidad de estas funciones de la red y se escriben a continuación:

1. El grado del numerador de F(s) no debe exceder el grado del denominador por más de la unidad. En otras palabras, (m n) debe ser menor o igual a uno.
2. F(s) no debe tener múltiples polos en el eje j o en el eje y de la trama polo-cero.
3. Las F(s) no deben tener postes en la mitad derecha del plano S.

Polinomio Hurwitz

Si sobre todo se cumplen los criterios de estabilidad (es decir, tenemos una función de red estable), entonces el denominador de la(s) F se denomina Polinomio Hurwitz.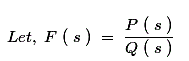

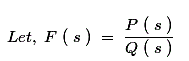
Donde, Q(s) es un Polinomio Hurwitz.

Propiedades de los polinomios de Hurwitz

Hay cinco propiedades importantes de los polinomios de Hurwitz y están escritas a continuación:

1. Para todos los valores reales de s el valor de la función P(s) debe ser real.
2. La parte real de cada raíz debería ser cero o negativa.
3. Consideremos que los coeficientes del denominador de F(s) es bn, b(n-1), b(n-2). . . . b0. Aquí cabe señalar que bn, b(n-1), b0 debe ser positivo y bn y b(n-1) no debería ser igual a cero simultáneamente.
4. La continua expansión de la fracción par a la parte impar de la Polinomio Hurwitz debe dar todos los términos de cociente positivo, si el grado par es mayor o la expansión continua de la fracción de impares a la parte par del polinomio de Hurwitz debe dar todos los términos de cociente positivo, si el grado impar es mayor.
5. En caso de polinomio puramente par o puramente impar, debemos hacer fracción continua con el derivado del polinomio puramente par o puramente impar y el resto del procedimiento es el mismo que se menciona en el punto número (4).

De la discusión anterior concluimos un resultado muy simple, Si todos los coeficientes del polinomio cuadrático son reales y positivos, entonces ese polinomio cuadrático es siempre un polinomio Hurwitz.

Funciones reales positivas

Cualquier función en forma de F(s) será llamada como una función real positiva si cumplen estas cuatro condiciones importantes:

1. F(s) debería dar valores reales para todos los valores reales de s.
2. La P(s) debería ser un polinomio de Hurwitz.
3. Si sustituimos s = j entonces al separar las partes real e imaginaria, la parte real de la función debería ser mayor o igual a cero, es decir, debería ser no negativa. Esta es la condición más importante y la utilizaremos frecuentemente para averiguar si la función es positiva real o no.
4. Al sustituir s = j, F(s) debe poseer polos simples y los residuos deben ser reales y positivos.

Propiedades de la función real positiva

Hay cuatro propiedades muy importantes de funciones reales positivas y están escritas abajo:

1. Tanto el numerador como el denominador de la F(s) deben ser polinomios de Hurwitz.
2. El grado del numerador de F(s) no debe exceder el grado del denominador por más de la unidad. En otras palabras, (m-n) debe ser menor o igual a uno.
3. Si F(s) es una función real positiva, entonces la recíproca de F(s) también debería ser una función real positiva.
4. Recuerde que la suma de dos o más funciones reales positivas es también una función real positiva, pero en caso de diferencia puede ser o no una función real positiva.

A continuación se presentan las cuatro condiciones necesarias pero no suficientes para que las funciones sean una función real positiva y se escriben a continuación:

1. El coeficiente del polinomio debe ser real y positivo.
2. El grado del numerador de F(s) no debe exceder el grado del denominador por más de la unidad. En otras palabras, (m n) debe ser menor o igual a uno.
3. Los polos y ceros en el eje imaginario deben ser simples.
4. Consideremos que los coeficientes del denominador de F(s) es bn, b(n-1), b(n-2). . . . b0Aquí cabe señalar que bn, b(n-1), b0 debe ser positivo y bn y b(n-1) no debería ser igual a cero simultáneamente.

Ahora hay dos condiciones necesarias y suficientes para que las funciones sean una función real positiva y se escriben a continuación:

1. F(s) debe tener polos simples en el eje j y los residuos de estos polos deben ser reales y positivos.
2. La suma del numerador y el denominador de F(s) debe ser un polinomio de Hurwitz.