¿Qué es la trama de Bode
A La trama de Bode es un gráfico que se utiliza comúnmente en ingeniería de sistemas de control para determinar la estabilidad de un sistema de control. Un gráfico de Bode traza la respuesta de frecuencia del sistema a través de dos gráficos que el Gráfico de la magnitud de Bode (expresando la magnitud en decibelios) y la Gráfico de fase de Bode (expresando el cambio de fase en grados).
Las tramas de Bode fueron introducidas por primera vez en la década de 1930 por Hendrik Wade Bode mientras trabajaba en los laboratorios Bell en los Estados Unidos. Aunque las gráficas de Bode ofrecen un método relativamente simple para calcular la estabilidad del sistema, no pueden manejar funciones de transferencia con singularidades en el medio plano derecho (a diferencia de Criterio de estabilidad del níquel).
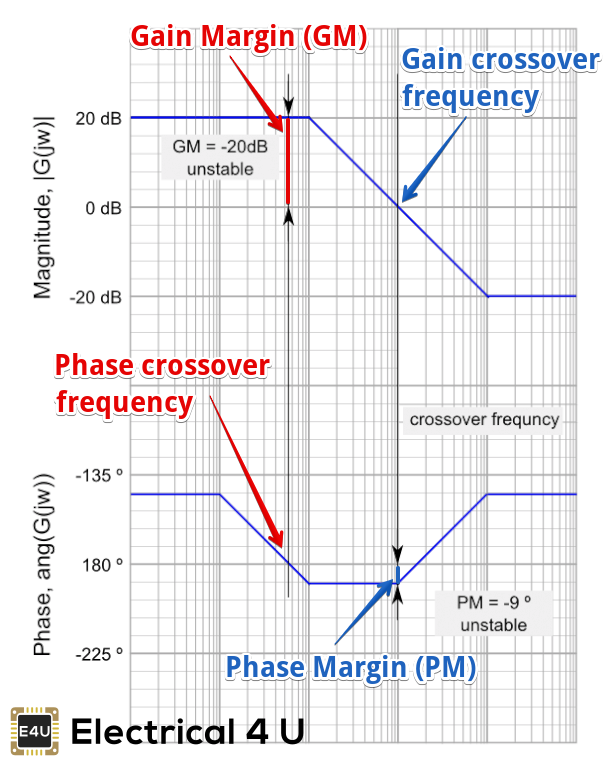

Comprensión márgenes de ganancia y márgenes de fase es crucial para entender las tramas de Bode. Estos términos se definen a continuación.
Ganancia de margen
Cuanto mayor sea el Ganancia de margen (GM), mayor será la estabilidad del sistema. El margen de ganancia se refiere a la cantidad de ganancia, la cual puede ser aumentada o disminuida sin hacer el sistema inestable. Se suele expresar como una magnitud en dB.
Por lo general, podemos leer el margen de ganancia directamente del gráfico de Bode (como se muestra en el diagrama anterior). Esto se hace calculando la distancia vertical entre la curva de magnitud (en el gráfico de magnitud de Bode) y el eje x en la frecuencia donde el gráfico de fase de Bode = 180. Este punto se conoce como el frecuencia de cruce de fase.
Margen de la fase
Cuanto mayor sea el Margen de la fase (PM), mayor será la estabilidad del sistema. El margen de fase se refiere a la cantidad de fase, que puede aumentarse o disminuirse sin hacer inestable el sistema. Normalmente se expresa como una fase en grados.
Normalmente podemos leer el margen de fase directamente del gráfico de Bode (como se muestra en el diagrama anterior). Esto se hace calculando la distancia vertical entre la curva de fase (en el diagrama de fase de Bode) y el eje x en la frecuencia donde el diagrama de magnitud de Bode = 0 dB. Este punto se conoce como el ganancia de la frecuencia de cruce.
Estabilidad de la parcela de Bode
A continuación se presenta una lista resumida de los criterios pertinentes para dibujar las parcelas de Bode (y calcular su estabilidad):
- Ganar Margen: Más grande será la margen de ganancia mayor será la estabilidad del sistema. Se refiere a la cantidad de ganancia, que puede ser aumentada o disminuida sin hacer el sistema inestable. Normalmente se expresa en dB.
- Margen de fase: Más grande será la margen de fase mayor será la estabilidad del sistema. Se refiere a la fase que puede ser aumentada o disminuida sin hacer el sistema inestable. Normalmente se expresa en fase.
- Ganar frecuencia de cruce: Se refiere a la frecuencia a la que la curva de magnitud corta el eje de cero dB en el gráfico de bode.
- Frecuencia de cruce de fases: Se refiere a la frecuencia con la que la curva de fase corta las veces negativas los 180o en esta trama.
- Frecuencia de la esquina: La frecuencia con la que las dos asíntotas se cortan o se encuentran se conoce como frecuencia de ruptura o frecuencia de esquina.
- Frecuencia de resonancia: El valor de la frecuencia a la que el módulo de G (j) tiene un valor de pico se conoce como la frecuencia de resonancia.
- Factores: Cada función de transferencia de bucle {i.e. G(s) H(s)} producto de varios factores como el término constante K, factores integrales (j), factores de primer orden ( 1 + jT)( n) donde n es un número entero, de segundo orden o factores cuadráticos.
- Pendiente: Hay una pendiente correspondiente a cada factor y la pendiente de cada factor se expresa en dB por década.
- Ángulo: Hay un ángulo correspondiente a cada factor y el ángulo de cada factor se expresa en grados.
Ahora hay algunos resultados que uno debe recordar para trazar la curva de Bode. Estos resultados están escritos a continuación:
- Término constante K: Este factor tiene una pendiente de cero dB por década. No hay ninguna frecuencia de esquina que corresponda a este término constante. El ángulo de fase asociado a este término constante también es cero.
- Factor integral 1/(j)n: Este factor tiene una pendiente de -20 n (donde n es cualquier número entero)dB por década. No existe una frecuencia de esquina correspondiente a este factor integral. El ángulo de fase asociado a este factor integral es de -90 n, donde n es también un número entero.
- Factor de primer orden 1/ (1+jT): Este factor tiene una pendiente de -20 dB por década. La frecuencia de esquina correspondiente a este factor es de 1/T de radián por segundo. El ángulo de fase asociado a este primer factor es -tan– 1(T).
- Factor de primer orden (1+jT): Este factor tiene una pendiente de 20 dB por década. La frecuencia de esquina correspondiente a este factor es de 1/T de radián por segundo. El ángulo de fase asociado a este primer factor es tan– 1(T) .
- Segundo orden o factor cuadrático: [{1/(1+(2/)} (j) + {(1/2)} (j)2)]: Este factor tiene una pendiente de -40 dB por década. La frecuencia de esquina correspondiente a este factor esn radián por segundo. El ángulo de fase asociado a este primer factor es
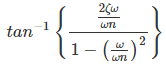
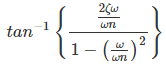
Cómo dibujar la trama de Bode
Teniendo en cuenta todos los puntos anteriores, somos capaces de dibujar un gráfico Bode para cualquier tipo de sistema de control. Ahora vamos a discutir el procedimiento para dibujar un gráfico de Bode:
- Sustituye la s = j en la función de transferencia de bucle abierto G(s) H(s).
- Encuentra las frecuencias de las esquinas correspondientes y tabúlalas.
- Ahora se requiere que un gráfico de semi-log elija un rango de frecuencia tal que el gráfico debe comenzar con la frecuencia que es más baja que la frecuencia de esquina más baja. Marque las frecuencias angulares en el eje x, marque las pendientes en el lado izquierdo del eje y marcando una pendiente cero en el centro y en el lado derecho marque el ángulo de fase tomando -180o en el medio.
- Calcule el factor de ganancia y el tipo u orden del sistema.
- Ahora calcula la pendiente correspondiente a cada factor.
Por dibujar el Gráfico de la magnitud de Bode:
- Marque la frecuencia de la esquina en el papel cuadriculado del semilogar.
- Tabula estos factores moviéndose de arriba a abajo en la secuencia dada.
- Término constante K.
- Factor integral
- Factor de primer orden
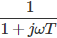
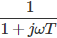
- Factor de primer orden (1+jT).
- Segundo orden o factor cuadrático:
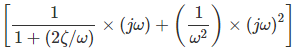
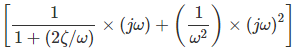
- Ahora esboza la línea con la ayuda de la correspondiente pendiente del factor dado. Cambie la pendiente en cada frecuencia de esquina añadiendo la pendiente del siguiente factor. Obtendrás la gráfica de la magnitud.
- Calcula el margen de ganancia.
Por dibujar el Gráfico de fase de Bode:
- Calcular la función de fase sumando todas las fases de los factores.
- Sustituir varios valores a la función anterior para averiguar la fase en diferentes puntos y trazar una curva. Obtendrás una curva de fase.
- Calcula el margen de fase.
Criterio de Estabilidad de Bode
A continuación se indican las condiciones de estabilidad:
- Para el sistema estable: Ambos márgenes deben ser positivos o el margen de fase debe ser mayor que el margen de ganancia.
- Para el Sistema Marginal Estable: Ambos márgenes deben ser cero o el margen de fase debe ser igual al margen de ganancia.
- Para el Sistema Inestable: Si alguno de ellos es negativo o margen de fase debería ser menor que el margen de ganancia.
Ventajas de la trama de Bode
- Se basa en la aproximación asintótica, que proporciona un método sencillo para trazar la curva de magnitudes logarítmicas.
- La multiplicación de varias magnitudes que aparece en la función de transferencia puede tratarse como una suma, mientras que la división puede tratarse como una resta, ya que estamos utilizando una escala logarítmica.
- Con la ayuda de esta trama sólo podemos comentar directamente la estabilidad del sistema sin hacer ningún cálculo.
- Gráficas de Bode proporciona una relativa estabilidad en términos de margen de ganancia y margen de fase.
- También abarca desde la gama de baja frecuencia hasta la de alta frecuencia.

Saludos. Tengo una duda especial con respecto a los criterios de estabilidad aquí mencionados: ¿Para qué casos se cumplen estos criterios? Para ilustrar mi duda postularé algunos ejemplos para que por favor me indiquen que casos corresponden a sistema estable y cuales a un sistema inestable:
GM= -15dB y MF= 48°
GM= 22dB y MF= -6°
GM= 12dB y MF= 35°
GM= -8dB y MF= -18°
Por lo que leo en el articulo hay que verificar el signo de ambos márgenes y además el valor del margen de fase con respecto al margen de ganancia.
Muchas Gracias y estaré atento a una respuesta.