El Teorema del Valor Inicial es una de las propiedades básicas de Laplace transformar. Fue dado por el prominente físico matemático francés Pierre Simon Marqués de Laplace. Hizo contribuciones cruciales en el área del movimiento planetario aplicando la teoría de la Gravitación de Newtons. Su trabajo sobre la teoría de la probabilidad y la estadística se considera pionero y esto influyó en toda una nueva generación de matemáticos. Laplace es una de las 72 personas que tienen su nombre grabado en la Torre Eiffel.
El teorema de valor inicial y el teorema de valor final se denominan conjuntamente como teoremas limitantes. El teorema del valor inicial se suele denominar IVT. Nos permitirá encontrar el valor inicial en el momento t = (0+) para una determinada función transformada (laplace) sin que nos permita trabajar más duro para encontrar f(t), lo cual es un proceso tedioso en tal caso.
Condiciones para la existencia del teorema del valor inicial
-
- La función f(t) y su derivada f(t) deben ser transformables en Laplace.
- Si el tiempo t se aproxima a (0+) entonces la función f(t) debería existir.
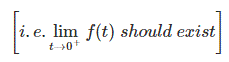
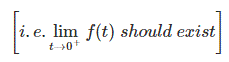
- La función f(t) = 0 para t > 0 y no contiene impulsos o singularidades de orden superior en el origen.
Declaración del Teorema del Valor Inicial de Laplace
Si f(t) y F(s) es Laplace transforman los pares, es decir
entonces el teorema del valor inicial está dado por
Prueba del teorema del valor inicial de Laplace
La transformación de una función f(t) es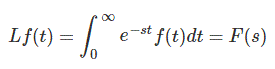
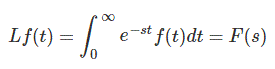
entonces la transformación de Laplace de su derivado f (t) es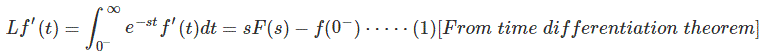
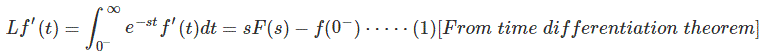
Considere primero la parte integral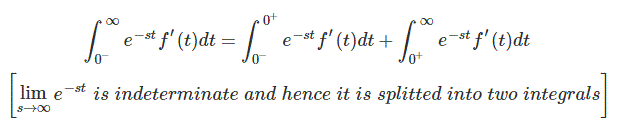
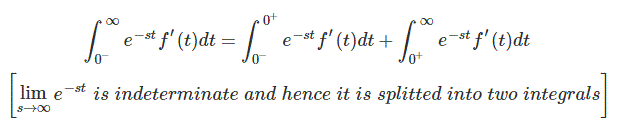
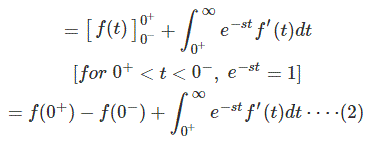
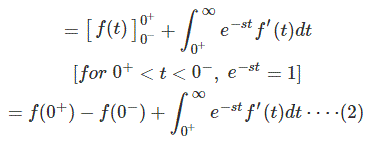
Sustituyendo (2) por (1) obtenemos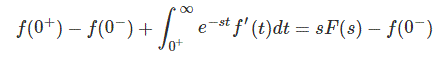
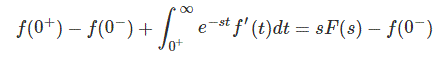
Al cancelar f (0)–) en ambos lados tenemos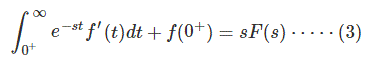
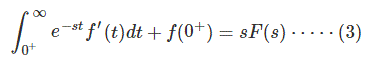
Podemos escribir inmediatamente la ecuación anterior, pero mi intención de tomar los límites de la integración de (0)– a ) es que, sin embargo, consideramos que los valores negativos de los límites pertenecen a los resultados que tienen valores positivos.
Nota:
También sabíamos que la transformación de Laplace sólo es aplicable a las funciones causales.
Al considerar (s) tiende al infinito en ambos lados en (3)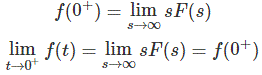
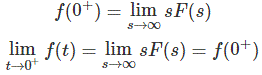
Por lo tanto, el teorema del valor inicial está probado.
Aplicaciones del Teorema del Valor Inicial
Como dije antes, el propósito del teorema del valor inicial es determinar el valor inicial de la función f (t) siempre que se dé su transformación de Laplace
Ejemplo 1 :
Encuentra el valor inicial de la función f (t) = 2 u (t) + 3 costo u (t)
Sol: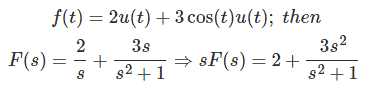
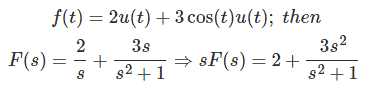
Por el teorema del valor inicial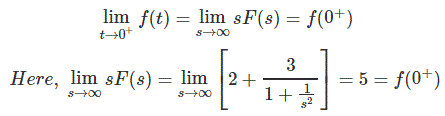
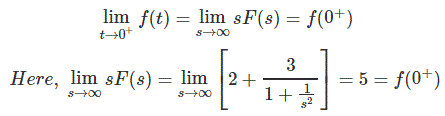
El valor inicial está dado por 5.
Ejemplo 2:
Encontrar el valor inicial de la función transformada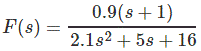
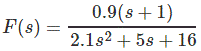
Sol: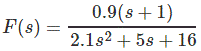
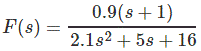
Por el teorema del valor inicial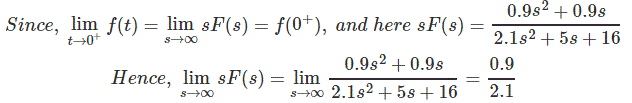
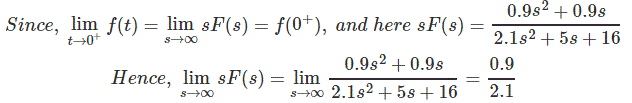
[a medida que los valores de s se vuelven cada vez más insignificantes, por lo que el resultado se obtiene simplemente tomando la proporción del coeficiente de plomo]
Ejemplo 3:
Encuentra el valor inicial de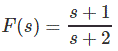 
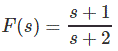
Solución:
El teorema del valor inicial no es aplicable en este caso. Podemos probarlo de dos maneras.
Veamos cómo va
Método 1: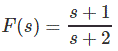
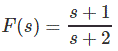
Nota:
Este teorema es aplicable estrictamente si F(s) es la fracción adecuada, es decir, el polinomio numerador es de orden inferior al polinomio denominador.
En caso de que se aplique el IVT obtenemos como valor inicial.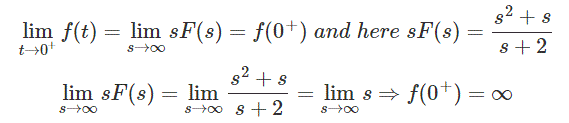
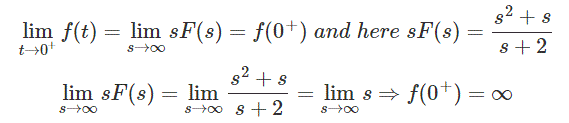
[esto no es posible en los circuitos prácticos]
Aliter: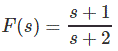
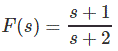
Aplicando la transformación de Laplace inversa
Es obvio que el teorema del valor inicial no es aplicable ya que existe una función de impulso, que es constante a lo largo del tiempo t.
Por esta discusión, es fácil para uno manipular las condiciones iniciales del circuito con la función transformada de Laplace.
